跳到主要内容

第8天 还记得大明湖畔的变量和函数吗

【教孩子学 Python 编程】系列 Day8：编写温度转换程序，了解变量、函数概念

不知不觉，我们已经一起写了好几个程序了。在编写程序的时候，很抱歉有些东西我刻意隐瞒了，因此今天我要停下来，给你讲讲当年大明湖畔的夏... 呸，变量和函数！

二元一次方程​

我们知道温度的单位有摄氏度和华氏度，它们之间的关系是：

F=C×1.8+32F = C × 1.8 + 32

其中，F 表示华氏温度，C 表示摄氏温度。

为了看起来舒服点，我们用 x 替换 C，用 y 替换 F。于是得到 y = 1.8x + 32 这样一个二元一次方程。

我们可以简写为函数关系式 y = f(x)

其中 x 是自变量，y 是因变量，此式表示 y 随 x 的变化而变化。而如何变化的秘密就藏在函数 f()，在这里也就是 y = 1.8x + 32 的关系。

所以，我们可以把自变量看成 “原因”，因变量看成 “结果”，函数看成是它们之间的 “关系”。

以上是数学上关于变量和函数的概念，计算机编程中变量和函数的概念也类似，但多了一些扩展。

同样是函数表达式 y = f(x) ，自变量 x 在程序中称为 “输入”，因变量 y 在程序中称为 “输出”。函数 f() 是中间处理过程，我们可以把它当成黑箱子，对于函数的使用者来说，通常只关心 “输入什么，就会输出什么” 的问题。

在程序设计中，自变量 x 也被称为 “参数”，因变量 y 则被称为 “返回值”。因此你可能会听到这样的描述：传入了参数 x，调用了函数 f()，返回了结果 y。

你的第一个Python函数​

我们用之前学的编程知识来实现摄氏温度和华氏温度的转换：

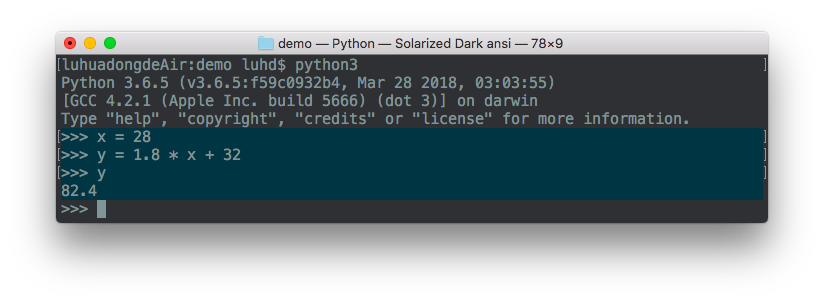
x = float(input("请输入摄氏温度值："))
y = 1.8 * x + 32
print("对应的华氏温度值为：", y)

第一行中的 float() 函数表示将输入的数值转换为浮点数（也就是小数）。

接下来，我们用函数来实现：

def f(Ce):
    F = 1.8 * Ce + 32
    return F

x = float(input("请输入摄氏温度值："))
y = f(x)
print("对应的华氏温度值为：", y)

前三行就是函数的实现，Python 中的函数使用 def 来标识（def 是 define 的缩写），这个函数的功能是接收一个参数 Ce，经过转换得到 F，并将 F 返回给使用者。

在看看倒数第二行，是不是很熟悉？这不就是前面的函数表达式 y = f(x) 吗？在程序中，我们称为函数的调用，函数内部转换后的 F 就会传递给变量 y。

当然，函数的名字不总是叫 f，我们通常会根据函数的功能取一个恰当的名字。比如这个温度转换函数可以取名为 temp_convert 或者 Ce2F。

IPO 编程模型​

还有点时间，再来讲一下 IPO 编程模型。IPO 模型是程序的基本编写方法，IPO 三个字母的含义如下：

  • I：Input 输入，程序的输入。
  • P：Process 处理，程序的主要逻辑。
  • O：Output 输出，程序的输出。

IPO 方法讲解的是，在编写程序的时候，我们要关注输入是什么，输出是什么，如何从输入达到输出。

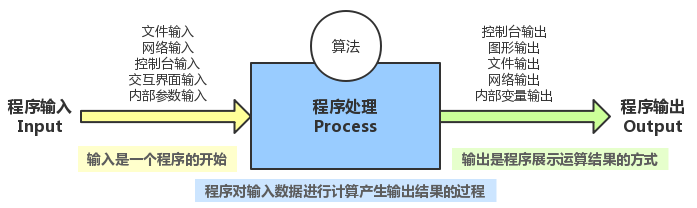
  • 程序的输入：文件输入、网络输入、控制台输入、交互界面输入、内部参数输入等。输入是一个程序的开始
  • 程序的输出：控制台输出、图形输出、文件输出、网络输出、操作系统内部变量输出等。输出是程序展示运算结果的方式。
  • 程序处理：程序对输入数据进行计算产生输出结果的过程。处理方法统称为算法，它是程序最重要的部分（算法是一个程序的灵魂）。

一个程序可以有零个或多个输入，至少一个或多个输出。没有输出的程序是没有意义的。

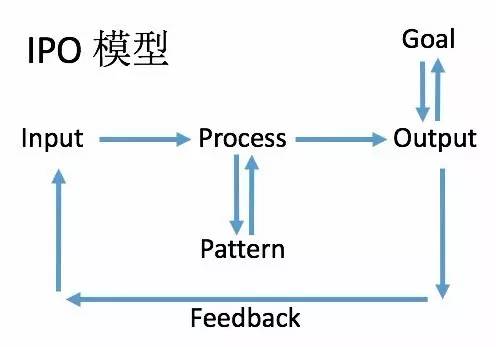
进一步抽象，你会发现，这种 IPO 模型同样适用于我们人本身。每个人的人生都是 获取信息输入-大脑处理-总结输出 的一个过程。

比如当你面对考试时，考试成绩就是你的输出，平时的学习积累就是你的输入。比如对于现在的我来说，写东西就是最终的输出，输入就是我前面的经验和瞎想。

其实每件事都一样，最终的结果无外乎就是看 “有什么输入” 和 “怎样处理”。

如果你感觉迷茫，难以输出，也许是因为输入不够。这时候就要多读书多看报，少吃零食多睡觉！

Quality input ensures quality output

同时，我们人类的大脑处理方式有无数多种，每个人要理解这个世界，都需要自己找到底层的思维模型。通过建立思维模型，形成自己独特、高效的处理方法。

编程解决问题的步骤​

  1. 分析问题：分析问题的计算部分（想清楚）
  2. 划分边界：划分问题的功能边界（规划 IPO）
  3. 设计算法：设计问题的求解算法（关注算法）
  4. 编写程序：编写问题的计算程序（编程序）
  5. 调试测试：调试程序使正确运行（运行调试）
  6. 升级维护：适应问题的升级维护（更新完善）

精简步骤

  • 确定IPO：明确计算部分及功能边界
  • 编写程序：将计算求解的设计变成现实
  • 调试程序：确保程序按照正确逻辑能够正确运行

程序是如何运行的​

Python 是一门解释型语言。额...... 怎么说呢，虽然电脑是我们的好朋友，但是我们和电脑其实很难沟通，比如我们要吃饭才有力气学习，电脑居然不用吃饭。所以就很难玩到一起去，但是我们又想和电脑沟通，让她帮我们做点事情，那怎么办？

那就用 Python 呀！Python 解释器就像一个翻译专家，我们把脑海中的想法和意图用 Python 语言写出了，然后交给 Python 解释器。她就会将帮我们检查并翻译成电脑看得懂的语言，之后电脑就会执行相应的操作，比如数字计算、字符打印等等。

作业​

（1）自己动手用函数的方式实现摄氏度和华氏度的转换程序。

（2）找一找到目前为止我们一共用过多少个函数。

（3）理解 IPO 编程模型。

详细讲解如何实现温度转换​

提出问题。

IPO 分析法​

划分边界

  • 输入：带华氏或摄氏标志的温度值
  • 处理：根据温度标志选择适当的温度转换算法
  • 输出：带摄氏或华氏标志的温度值

输入输出格式要求：标识放在温度值的后面，F 表示华氏度，C 表示摄氏度。

比如：82F 表示华氏82度，28C 表示摄氏28度。

设计算法​

根据华氏和摄氏温度的定义，可得如下转换公式：

C=F−321.8{C = \frac{F - 32}{1.8}}

F=C×1.8+32{F = C \times 1.8 + 32}

其中，C 表示摄氏温度，F 表示华氏温度。

判断键盘输入的是否为数字​

num = input("请输入一个数字：")
if

将代码写到文件中​

简单点：输入摄氏温度，输出华氏温度

"""
 文件：Ce2F.py
 描述：将摄氏温度转换为华氏温度
"""

C = input("请输入摄氏温度值：")
F = 1.8 * float(C) + 32
print("对应的华氏温度为：{:.2f}".format(F))
"""
 文件：TempConvert.py
 描述：实现华氏和摄氏温度的转换
"""

TempStr = input("请输入带有符号的温度值：")

if TempStr[-1] in ['F', 'f']:
    C = (eval(TempStr[0:-1]) - 32)/1.8
    print("转换后的温度是 {:.2f}C".format(C))
elif TempStr[-1] in ['C', 'c']:
    F = 1.8 * eval(TempStr[0:-1]) + 32
    print("转换后的温度是 {:.2f}F".format(F))
else:
    print("输入格式错误")

运行 Python 程序​

代码说明​

  • 我们在编辑器中输入代码，发现代码会呈现不同的颜色，这种效果称为代码高亮，目的让我们看得舒服点。代码高亮是编程的色彩辅助体系，不是语法要求，因此在不同的编辑器中，代码高亮的表现形式各有不同。
  • 缩进是一行代码开始前的空白区域，表达程序的格式框架
    • 严格明确：缩进是语法的一部分，缩进不正确程序运行错误
    • 所属关系：表达代码间包含和层次关系的唯一手段
    • 长度一致：程序内一致即可，一般用4个空格或1个Tab
  • 注释是提高程序可读性的方式，注释是不被程序执行的辅助性说明信息
    • 单行注释：以 # 开头，其后内容为注释
    • 多行注释：以 ''' 开头和结尾